大家都知道费波那契数列的定义是:
- F = 0
- F1 = 1
- Fn = Fn-1 + Fn-2
如果直接按照这个定义来计算效率是很低的。所有,为获得第 n 个数,一般都会采用迭代的方式计算整个 0-n 的斐波那契数列,在 n 比较小的时候(小于十万)效率还是很不错的(在我的机器上 Java 程序计算 F100000耗时 1s)。但如果仅仅是为了获得第 n 个数,这又显得太低效了。这种时候就适合使用通项公式来计算:
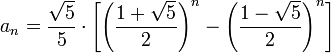
公式的推导过程可以参考:http://en.wikipedia.org/wiki/Fibonacci_number。
算法分析
为了方便讨论,设:
a = [1 + sqrt(5)] / 2
b = [1 + sqrt(5)] / 2
fib(n) = (a^n - b^n) / sqrt(5)
= (a^n - b^n) / (a - b)
如果直接按照这个公式来写程序,需要分别a和b两个数的n次幂。
减少求幂次数
但容易发现:
a = -1 / b
即
fib(n) = (a^n - (-1/a)^n) / (a - (-1/a))
因此,只需求a的n次幂,再通过一次求倒数运算就得到b,计算量减少一半。
快速求幂
朴素的求幂算法效率为O(n),即迭代n次。根据规则:
x^n = x^(n/2) * x^(n/2) ; 当n是偶数
x^n = x^(n/2) * x^(n/2) * x ; 当n是奇数
可以把效率提升到O(log2n),在《JavaScript字符串乘法》一文中也使用了类似的技巧。
虚数的乘法
我们发现a是无理数,而计算结果fib(n)是一个正整数,如果直接使用[1 + sqrt(5)] / 2做乘法,就会有相应的精度丢失。为了避免精度丢失,把sqrt(5)想象成一个虚数i,即1/2 + 1/2i,其中实部和虚部都是1/2。虚数的乘法规则如下:
(x + y * i) * (m + n * i)
= (x * m + y * n * i * i) + (x * n + y * m) * i
= (x * m - y * n) + (x * n + y * m) * i
对应到a,即i = sqrt(5)就是:
(x * m + 5 * y * n) + (x * n + y * m) * sqrt(5)
Clojure版
本来是想着用 Java 写一个,一想到又要定义两三个类代码会显得冗长,倒不如用 Clojure 来实现。好在 Clojure 里也没太多稀奇古怪的符号,即使你没接触过 Clojure,应该还是能看懂。
(ns redraiment.math.fibonacci
"Some utils for generate fibonacci number.")
(def ^{:private true :dynamic true} *base*
"Base number for composite number.
As you know, it's complex when *base* = -1."
5)
(defn- multiply
"Returns the product of composite nums. Supports arbitrary precision.
(multiply) returns [1 0]."
[& args]
(reduce
#(let [a1 (first %1)
b1 (second %1)
a2 (first %2)
b2 (second %2)]
[(+ (* a1 a2) (* b1 b2 *base*))
(+ (* a1 b2) (* a2 b1))])
(cons [1 0] args)))
(defn- pow
"Returns a composite num whose value is c^n."
[c n]
(cond
(== n 0) [1 0]
(== n 1) c
(> n 1) (let [sub (pow c (quot n 2))]
(multiply sub sub (if (odd? n) c [1 0])))
:else (throw (IllegalArgumentException.
"n MUST be a natural number"))))
(defn fibonacci-nth
"Returns the n-th fibonacci in high performance.
The algorithm is: fib(n) = (a^n - b^n) / (a - b)
where a = (1 + sqrt(5)) / 2 and b = -1 / a.
See http://en.wikipedia.org/wiki/Fibonacci_number."
[n]
(* (second (pow [1/2 1/2] n)) 2))
计算第一百万个斐波那契数,耗时 4秒。大家可以自己试试用迭代法计算,在我的电脑上耗时 1分钟:
redraiment.math.fibonacci=>(time (do (fibonacci-nth 1000000) 0))
"Elapsed time: 4272.027189 msecs"
0
Scheme版本
有网友把上面的代码翻译成Scheme,据他说代码执行效率很低。我试着在我本地用 Guile 或 Kawa 来执行他的代码,都提示 Out Of Memory。但我一直相信 Scheme 的性能会更好,因为它的解释器是 C语言实现的,Clojure 则运行在 JVM 下的。所以我就自己翻译了一下之前的代码,也是计算第1000000个斐波那契数,在我公司这台旧电脑上的执行效率远好于Clojure版:
$ time guile fib.scm
1953282128707757731632.......42546875
real 0m0.750s
user 0m0.265s
sys 0m0.124s
代码如下
(define (c* a b)
(let ((a1 (car a))
(b1 (cadr a))
(a2 (car b))
(b2 (cadr b)))
(list (+ (* a1 a2) (* b1 b2 5))
(+ (* a1 b2) (* a2 b1)))))
(define (c** r i c)
(if (zero? c)
r
(c** (if (odd? c) (c* r i) r)
(c* i i)
(quotient c 2))))
(define (fib n)
(* 2 (cadr (c** '(1 0) '(1/2 1/2) n))))
(display (fib 1000000))