杨辉三角形,又称贾宪三角形、帕斯卡三角形,是二项式系数在三角形中的一种几何排列。其中第n行第i列的值为:Cin= n!/(i! * (n - i)!)。如下图所示。
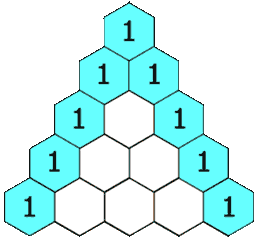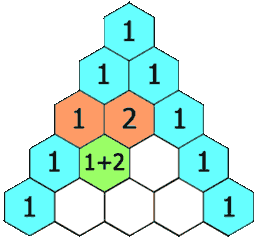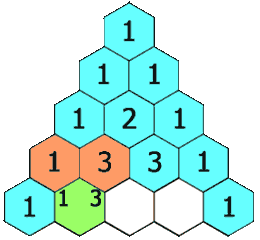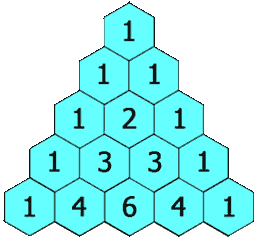
为了输出一个规模为n的杨辉三角,如果根据定义来做,那每一个元素至少要计算两个阶乘,效率是很低的。从下图可知,第i行可以通过第i-1行的元素两两相加得到,这样乘法就简化成一组加法,效率会提高很多!
如果你了解函数式编程,可能知道map和reduce两个运算符:map可以保持数据维度不变,reduce则把一个n维的数据降到1维。杨辉三角属于第三类范畴:把维度为1的数据扩展成n维。
本文提供多种不同的编程语言的解决方法,来比较各语言解决此类问题的优劣。
Clojure版
(defn pascal []
(iterate #(map + `(0 ~@%) `(~@% 0)) [1]))
(take 5 (pascal)) ; 取前面5行
; ->((1) (1 1) (1 2 1) (1 3 3 1) (1 4 6 4 1))
Clojure版是这么多实现中最简洁、最优雅的!
- 通过内置的倒引号操作符,非常简便地在原数组前后两端追加额外的数据
0,达到扩展维度的目的; - 利用现成的迭代工具
iterate,无需关心迭代过程,只需专注于每次迭代的逻辑; - 惰性列表让程序无需关心何时结束。
Common Lisp 版
(do ((a '(1) (mapcar #'+ `(0 ,@a) `(,@a 0))))
((= (length a) 10))
(format t "~{~A~^ ~}~%" a))
Common Lisp拥有和Clojure相同的倒引号功能,但没有类似iterate的自动迭代工具,因此不得不使用do手工控制迭代过程以及结束条件。但Common Lisp优雅的format输出功能,是其他语言可欲而不可求的!
Python版
from operator import add
def pascal(n):
a = [1]
for i in range(n):
yield a
a = map(add, [0] + a, a + [0])
[a for a in pascal(10)]
适合Python 2.*版本,Python的特色是Yield生成器与列表推导。
C语言版
#include <stdlib.h>
#include <stdio.h>
#define SIZE 11
int main(void) {
int line[SIZE] = {1};
int row;
int i;
for (row = 0; row < SIZE; row++) {
for (i = row; i > 0; i--) {
line[i] += line[i - 1];
}
for (i = 0; i <= row; i++) {
printf("%d%c", line[i], i == row? '\n': ' ');
}
}
return EXIT_SUCCESS;
}
- C语言不能像Lisp那样便捷地生成新数组,因此一开始就开辟好足够的空间;
- 该版本忠实地反映出当前行如何由前一行的数据生成;
- C语言同样没有直接输出数组的能力,因此不得不采用循环来打印每一行;
- C的繁琐换来的是高性能。
批处理版
::Show a Pascal/Yanhui Triangle
@echo off
setlocal enabledelayedexpansion
set /a line[0]=1
for /l %%i in (0,1,10) do (
for /l %%j in (%%i,-1,1) do (
if defined line[%%j] (
set n=%%j
call :calc
) else (
set /a line[%%j]=1
)
)
for /l %%j in (0,1,%%i) do set /p=!line[%%j]! <nul
echo.
)
goto end
:calc
set /a prev=%n%-1
set /a line[%n%]+=!line[%prev%]!
goto :eof
:end
pause
还是那句话:不要小看批处理!虽然它……很蛋疼。
Bash 版
#!/usr/bin/bash
a[0]=1
for ((i=0;i<=10;i++)); do
for ((j=$i;j>0;j--)); do
((a[$j]+=a[$j-1]))
done
for ((j=0;j<=$i;j++)); do
printf "%d " ${a[$j]}
done
echo
done
批处理都来了,怎么能少的了Shell Script。