问题描述

Problem Description

在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的：

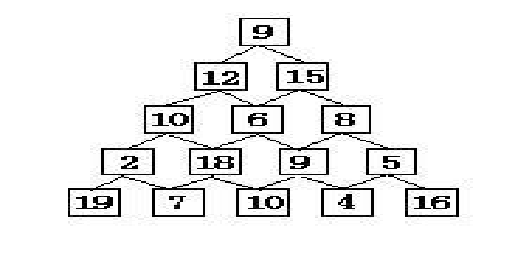
有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

已经告诉你了，这是个DP的题目，你能AC吗?

Input

输入数据首先包括一个整数C,表示测试实例的个数，每个测试实例的第一行是一个整数N(1 <= N <= 100)，表示数塔的高度，接下来用N行数字表示数塔，其中第i行有个i个整数，且所有的整数均在区间[0,99]内。

Output

对于每个测试实例，输出可能得到的最大和，每个实例的输出占一行。

Sample Input

1
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

Sample Output

30

问题分析

Problem Analyse

二维数组上的动态规划

Algorithm Analyse

前面已经做过两道一维数组上的动态规划。二维数组上的动态规划就是一个递归的过程了。

我们知道，在求解的过程中，很多元素的值都算了不止一次，所有我们可以开个数组把这些已经计算出来的中间值保存下来。这就是编程的又一大原则:以空间换时间。我们把原来的数塔保存入一个二维数组g[n][n]里

f[i][j] = g[i][j] + max(f[i+1][j], f[i+1][j+1]) (i < n)
f[i][j] = g[i][j] (i = n)

最后我们输出f[0][0]就可以了。下面给出动态规划的AC代码:

#include <stdio.h>
#include <string.h>

#define max(a,b) (a)>(b)?(a):(b)

int  f[120][120];
int  g[120][120];
int  n;

int fc(int i,int j)
{
  if(f[i][j]==-1)
    f[i][j]=i==n-1?g[i][j]:max(g[i][j]+fc(i+1,j),g[i][j]+fc(i+1,j+1));
  return f[i][j];
}

int main(void)
{
  int  c;
  int  i;
  int  j;
  
  scanf("%d", &c);
  while (c--)
  {
    memset(f,-1,sizeof(f));
    scanf("%d",&n);
    for(i=0;i<n;i++)
    {
      for(j=0;j<=i;j++)
        scanf("%d",&g[i][j]);
    }
    printf("%d\n",fc(0,0));
  }
  return 0;
}

但其实这一题完全可以不用动态规划。我们从最下层往上推，比如到了第i层，比较f(i, j)和f(i, j+1)，把较大值加到f(i-1, j)上。事实证明，这样算的速度比动态规划要快。

算法实现

这是一个下三角矩阵，直接开二维数组太浪费空间了。可以开个一维数组压缩空间。

参考源码