问题描述
Problem Description
小兔的叔叔从外面旅游回来给她带来了一个礼物,小兔高兴地跑回自己的房间,拆开一看是一个棋盘,小兔有所失望。不过没过几天发现了棋盘的好玩之处。从起点(0,0)走到终点(n,n)的最短路径数是C(2n,n),现在小兔又想如果不穿越对角线(但可接触对角线上的格点),这样的路径数有多少?小兔想了很长时间都没想出来,现在想请你帮助小兔解决这个问题,对于你来说应该不难吧!
Input
每次输入一个数n(1<=n<=35),当n等于-1时结束输入。
Output
对于每个输入数据输出路径数,具体格式看Sample。
Sample Input
1
3
12
-1
Sample Output
1 1 2
2 3 10
3 12 416024
问题分析
Problem Analyse
递推题
Algorithm Analyse
我们假设小兔的棋盘是8×8的(当然你也可以假设是其他)。如下图:
箭头方向表示从该格子下一步能去的格子。因为不能穿越对角线,所有对角线上的格子只有进去的箭头,没有出来的箭头。
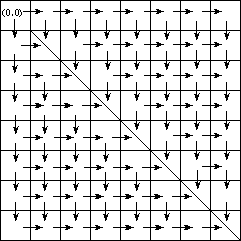
观察上图你就可以发现,其实这是一张关于对角线对称的图。所有我们只要求一个方向的值,然后乘以2即可。
我们就拿下三角来考虑。不难发现,所有在0列上的格子,路径数都是1(只能从上面过来)。
而其他格子则都是由上、左两个方向过来,即:f(i, j) = f(i - 1, j) + f(i, j - 1);
另外f(i, i) = f(i, j - 1);
算法实现
规律我们是找到了,但不用急着编程。虽然它是用一个矩阵描述的,但我们大可不必开一个二维数组。我们只要开一个一维数组就可以了。因为f(i, j) = f(i, j - 1) + f(i - 1, j); 而我们做完第i-1趟处理后,保存的是第i-1行上的数据。相当于已经有了f(i - 1, j),所有只要在原来的基础,就是加上它左边的数就可以了。