问题描述
Problem Description
虽然草儿是个路痴(就是在杭电待了一年多,居然还会在校园里迷路的人,汗~),但是草儿仍然很喜欢旅行,因为在旅途中 会遇见很多人(白马王子,^0^),很多事,还能丰富自己的阅历,还可以看美丽的风景……草儿想去很多地方,她想要去东京铁塔看夜景,去威尼斯看电影,去阳明山上看海芋,去纽约纯粹看雪景,去巴黎喝咖啡写信,去北京探望孟姜女……眼看寒假就快到了,这么一大段时间,可不能浪费啊,一定要给自己好好的放个假,可是也不能荒废了训练啊,所以草儿决定在要在最短的时间去一个自己想去的地方!因为草儿的家在一个小镇上,没有火车经过,所以她只能去邻近的城市坐火车(好可怜啊~)。
Input
输入数据有多组,每组的第一行是三个整数T,S和D,表示有T条路,和草儿家相邻的城市的有S个,草儿想去的地方有D个;
接着有T行,每行有三个整数a,b,time,表示a,b城市之间的车程是time小时;(1=<(a,b)<=1000;a,b 之间可能有多条路)
接着的第T+1行有S个数,表示和草儿家相连的城市;
接着的第T+2行有D个数,表示草儿想去地方。
Output
输出草儿能去某个喜欢的城市的最短时间。
Sample Input
6 2 3
1 3 5
1 4 7
2 8 12
3 8 4
4 9 12
9 10 2
1 2
8 9 10
Sample Output
9
问题分析
求单源最短路径的算法是Dijkstra算法。它解决了有向图G=(V, E)上带权的单源最短路径问题。但要求所有边的权值非负。
Dijkstra算法中设置了一顶点集合S,从源点s到集合中的顶点的最终最短路径的权值均已确定。算法反复选择具有最短路径估计的顶点u∈V-S,并将u加入到S中,对u的所有出边进行松弛。在下面的 算法实现中,用到了顶点的最小优先级列队Q,排序关键字为顶点的d值。
下面是Dijkstra的伪码:
DIJKSTRA(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s)
2 S←Φ
3 Q←V[G]
4 while Q ≠ Φ
5 do u ← EXTRACT-MIN(Q)
6 S ← S∪{u}
7 for each vertex v ∈ Adj[u]
8 do RELAX(u, v, w)
下面用来演示一下它的执行过程。正确性这里就不证明了。
 |
 |
 |
| a | b | c |
 |
 |
 |
| d | e | f |
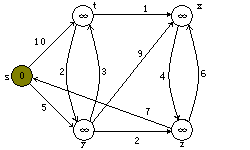
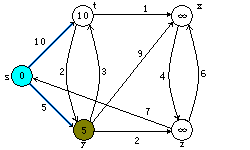
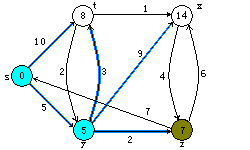
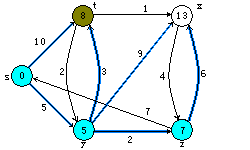
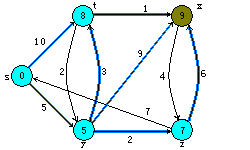
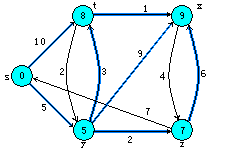
Dijkstra算法的执行过程。源点s为最坐端顶点。最短路径估计被标记在顶点内,阴影覆盖的边指出了前趋的值。 蓝色顶点在集合S中,而白色顶点在最小优先级队列Q=V-S中。 a)第4~8行while循环第一次迭代前的情形。阴影覆盖的顶点具有最小的d值,而且在第5行被选为顶点u。 b)至f)while循环在每一次连续迭代后的情形。每个图中阴影覆盖的顶点被选作下一次迭代第5行的顶点u。 f)图中的值为最终结果。
因为Dijkstra算法总是在V-S中选择“最轻”或“最近”的顶点插入集合S中,所有我们说它使用了贪心策略。
算法实现
最小优先级队列可以用STL里的make_heap()来。下面是C++版的Dijkstra算法。
struct node {
int ord;
int cost;
} v[1001];
for (i = len; i; i--) {
make_heap(v + 1, v + 1 + i);
for (j = 2; j <= i; j++) {
if (v[j].cost > v[1].cost + mp[v[1].ord][v[j].ord])
v[j].cost = v[1].cost + mp[v[1].ord][v[j].ord];
}
swap(v[1], v[i]);
}
sort(v + 1, v + 1 + len, cmp);
但发现用STL,速度会比较慢,大概需要90几MS。我的参考代码里用的是数组。没用STL。