问题描述
Problem Description
Given two rectangles and the coordinates of two points on the diagonals of each rectangle,you have to calculate the area of the intersected part of two rectangles. its sides are parallel to OX and OY .
Input
Input The first line of input is 8 positive numbers which indicate the coordinates of four points that must be on each diagonal.The 8 numbers are x1,y1,x2,y2,x3,y3,x4,y4.That means the two points on the first rectangle are(x1,y1),(x2,y2);the other two points on the second rectangle are (x3,y3),(x4,y4).
Output
Output For each case output the area of their intersected part in a single line., accurate up to 2 decimal places.
Sample Input
1.00 1.00 3.00 3.00 2.00 2.00 4.00 4.00
5.00 5.00 13.00 13.00 4.00 4.00 12.50 12.50
Sample Output
1.00
56.25
问题分析
Problem Analyse
给出两个矩形在对角线上的顶点的坐标,要求你计算两个矩形的公共部分的面积。
数学计算。
Algorithm Analyse
两个矩形摆放大致有下面几种(其他几种都可以由它们变形过来)。
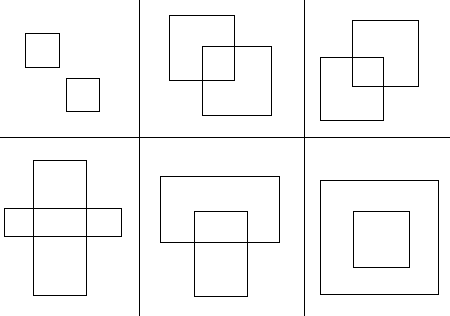
其实,说的极端一点,两矩形摆放,也就两种摆法:相交与不相交。
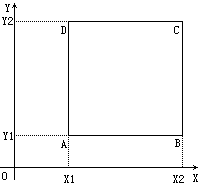
这一题这样考虑反而更简单一点。要求一个矩形的面积。如下图,我们先要知道边AD、BC的横坐标(X1, X2),边AB、CD的纵坐标(Y1, Y2)。然后按公式S = (X2 - X1) * (Y2 - Y1)。因此问题的关键是求这四个参数。

两个矩形相交的图形一定是矩形(这个容易证明,这里不阐述)。如下图,我们只要求出相交的矩形的那四个参数就可以了。
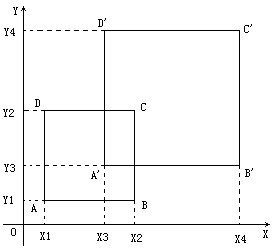
X1' = max(X1, X3)
Y1' = max(Y1, Y3)
X2' = min(X2, X4)
Y2' = min(Y2, Y4)
而当X1 > X2 且 Y1 > y2,则原来的两个矩形相离,所以面积为0。
算法实现
如下图:给出的两点可能是A、C,也可能是B、D,所以我们自己要在开始时做个统一。